介绍

在数学中，开根是乘方的逆运算，即

以二次方根为例:

由以上公式得知2=\sqrt{2^2}=\sqrt{4}.相反的,\sqrt{4}=2

在人类看来,算根号这类问题很容易解决,但是在计算机里,这却是一种难题,倒也不是不可以枚举乘方来算出结果,但是这样会消耗大量资源,例如:

如果要开根的数很大且带有小数点的话

直到...

即2753880.508324开方的结果为1659.482

这种方法无疑是非常耗费资源的,好在有一种方法能够比较快速的得到平方根,那就是牛顿法

牛顿法

牛顿法（英语：Newton's method）又称为牛顿-拉弗森方法（英语：Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。

-摘自 维基百科-牛顿法

它的公式是:

假设a是对方程f(x) = 0的解 (x)的一个近似.如果令

则在很多情况下,b是个比a更好的近似.

Adrian Banner. (2016). 13.3 牛顿法. In 杨爽 赵晓婷 高璞(Ed.),普林斯顿微积分读本(修正版)(pp. 258-259) 北京:人民邮电出版社

也就是说,如果我们知道\sqrt{2}在1和2之间,也就是它的近似值是1~2,那么通过牛顿法就能得出它的更好的近似 1.4 , 知道1.4之后通过牛顿法又能得到更近的近似值 1.41 ,以此往复.

以下是计算\sqrt{2}的完整过程:

设x为\sqrt{2}的解,最开始的近似值(a)为1,即

由此得\sqrt{2}的近似值为1.414

当然,要求n的次方根,它的函数为f(x)=x^2-n,当f(x)=0时,x即为开方结果.

原理

牛顿法很神奇,那么它的原理是什么呢?

以下按照f(x)=x^2-2(即开方\sqrt{2})来解释

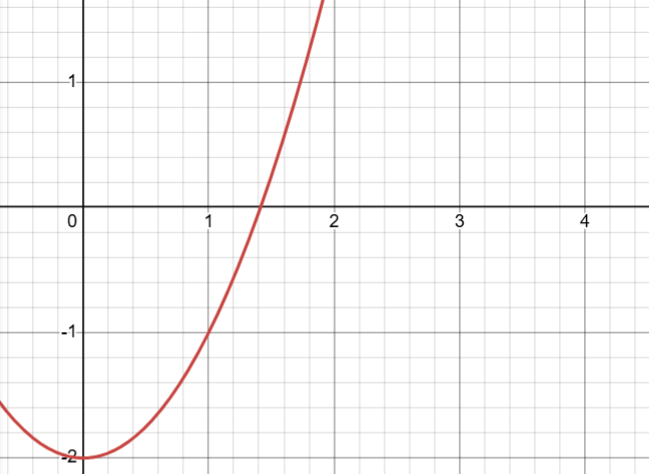
这是函数的一部分图像,我们来做函数x=1的切线

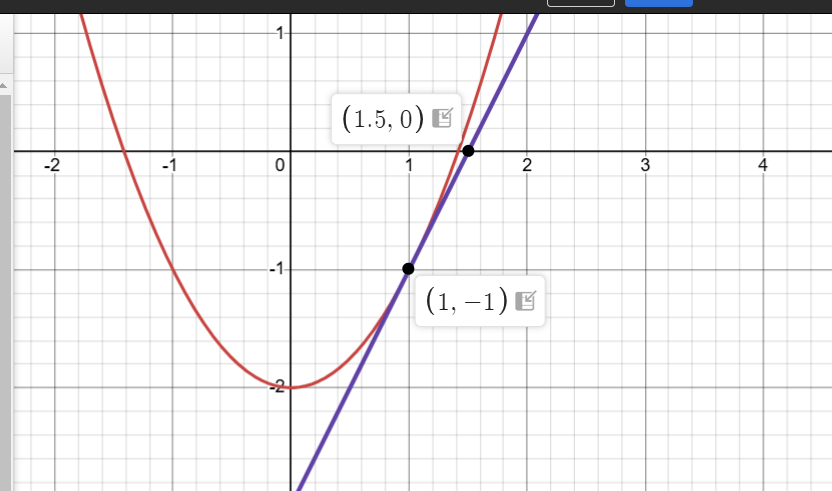
可见,当切线的y=0时,x即为f(x)=x^2-2=0的近似值,也就是\sqrt{2}的近似值, 接下来我们再以x=1.5做函数的切线 (注:图像有较小偏差)

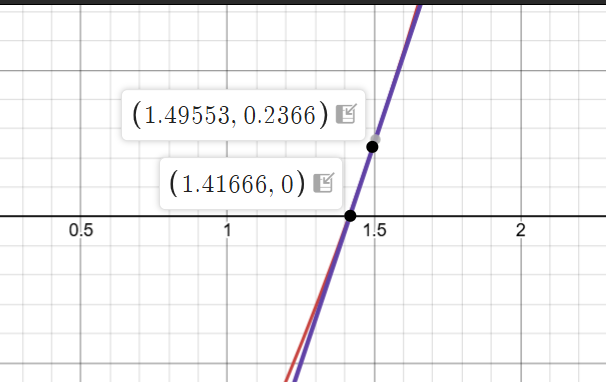
可见,当切线y=0时,x=1.41666,即\sqrt{2}的近似值是1.41666
想象一下: 我们拿一个直线紧贴着这个函数移动,会出现两个交点, 即与函数的交点和与x轴(y=0)的交点 ,如果这两个交点无限接近,这不就是这个函数的解了吗? 不就得出开根结果了吗

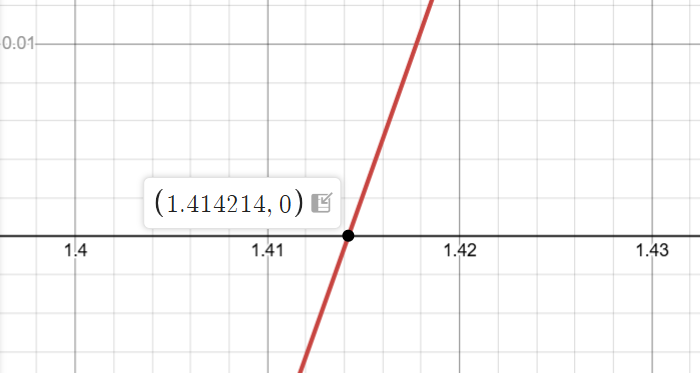
这就是牛顿法的原理,牛顿法在大部分函数适用,有个别函数不是用.如果有时间的话我会再次深析牛顿法.

编程写法

Python

num = int(input("要开方数: "))
a = int(input("最开始的近似值: "))
n = int(input("循环次数: "))

# 定义开方函数
def sqrt(num, a, n):
    for i in range(n):
        a = a - (a**2 - num) / (2 * a)
    return a

print(sqrt(num, a, n))

C/C++ (math.h库里已有sqrt函数，此代码为示范)

#include <stdio.h>

double sqrt(double num, double a, int n){
    for(int i=0;i<n;i++){
        a = a - (a*a - num) / (2 * a);
    }
    return a;
}

int main(){
    double num, a;
    scanf("%lf %lf", &num, &a);
    int n;
    scanf("%d", &n);

    printf("%lf",sqrt(num, a,n));
}